以太之光无敌无限钻石版

以太坊（Ethereum）使用椭圆曲线数字签名算法（ECDSA）来对交易进行签名。ECDSA是一种广泛使用的公钥加密算法，它基于椭圆曲线密码学。

在以太坊中，交易签名用于证明交易是由拥有相应私钥的用户发起的。交易签名由两部分组成：签名值（r, s）和恢复标识符（v）。签名值（r, s）是使用用户的私钥和交易数据生成的，而恢复标识符（v）用于确定交易发送者的公钥。

以下是ECDSA签名算法的简要概述：

1. 生成私钥和公钥：首先，用户需要生成一对私钥和公钥。私钥是一个随机数，必须保密，而公钥是从私钥派生出来的。

2. 生成签名：当用户想要发起一笔交易时，他们需要使用自己的私钥和交易数据来生成签名。这个过程包括以下几个步骤：

a. 计算交易数据的哈希值：首先，需要计算交易数据的哈希值。在以太坊中，通常使用SHA3（Keccak256）哈希算法。

b. 选择随机数k：选择一个随机数k，这个随机数在每次签名时都应该不同，以增加签名的安全性。

c. 计算签名值（r, s）：使用椭圆曲线算法，将随机数k和交易数据的哈希值结合起来，生成签名值（r, s）。

3. 确定恢复标识符（v）：恢复标识符（v）用于确定交易发送者的公钥。它可以从签名值（r, s）和随机数k中计算得出。

4. 验证签名：交易接收者可以使用发送者的公钥和交易数据来验证签名的有效性。如果签名有效，那么交易就是由拥有相应私钥的用户发起的。

请注意，以上内容仅提供了ECDSA签名算法的简要概述。在实际应用中，还需要考虑一些额外的安全措施，如防止重放攻击和中间人攻击等。

深入解析以太坊签名算法：原理与应用

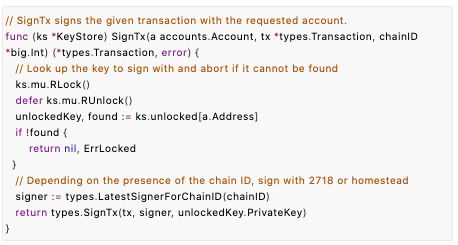
以太坊作为当前最流行的区块链平台之一，其安全性依赖于一系列复杂的加密算法。其中，签名算法是确保交易安全性的关键组成部分。本文将深入解析以太坊的签名算法，探讨其原理和应用。

一、以太坊签名算法概述

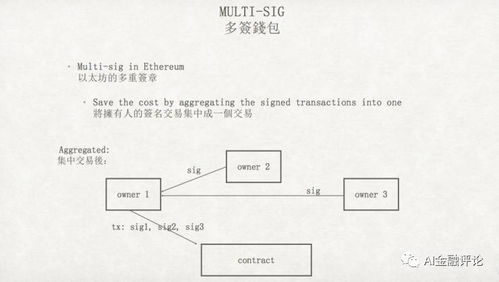
以太坊签名算法主要基于椭圆曲线数字签名算法（ECDSA）。ECDSA是一种公钥密码学算法，它利用椭圆曲线的数学特性来实现数字签名。在以太坊中，签名算法主要用于以下两个方面：

交易签名：用户在发送交易时，需要使用私钥对交易进行签名，以确保交易的真实性和不可篡改性。

合约调用：智能合约在执行过程中，需要验证调用者的身份，以确保合约的安全性。

二、以太坊签名算法原理

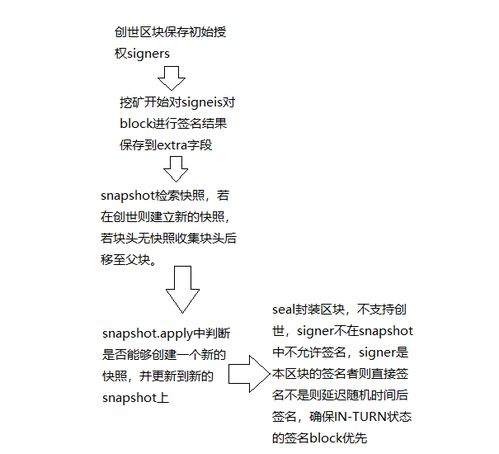
以太坊签名算法的原理如下：

私钥生成：用户首先生成一个私钥，私钥是一个随机选取的数字，用于签名和验证。

公钥推导：私钥可以通过椭圆曲线加密算法推导出公钥。公钥是公开的，用于验证签名。

签名生成：当用户发送交易或调用合约时，使用私钥对交易或合约调用进行签名。签名过程包括以下步骤：

消息散列：将交易或合约调用消息进行散列，得到一个固定长度的散列值。

生成随机数：生成一个随机数k，用于签名过程。

计算r和s：使用椭圆曲线加密算法和随机数k，计算r和s，r和s共同构成签名。

签名输出：将r和s输出作为签名。

验证签名：接收者使用发送者的公钥和签名，验证签名的有效性。

三、以太坊签名算法应用

以太坊签名算法在以下场景中得到了广泛应用：

交易签名：用户在发送以太币或ERC-20代币等交易时，需要使用私钥对交易进行签名，以确保交易的安全性。

智能合约调用：智能合约在执行过程中，需要验证调用者的身份，以确保合约的安全性。调用者使用私钥对合约调用进行签名，智能合约验证签名后，执行相应的操作。

身份验证：以太坊签名算法可以用于身份验证，例如在去中心化身份（DID）系统中，用户可以使用私钥对身份信息进行签名，以证明身份的真实性。

四、以太坊签名算法的优势

以太坊签名算法具有以下优势：

安全性：基于椭圆曲线加密算法，具有较高的安全性。

高效性：签名过程和验证过程较为高效，适用于大规模应用。

通用性：适用于各种场景，如交易签名、智能合约调用、身份验证等。

以太坊签名算法是确保以太坊平台安全性的关键组成部分。通过深入解析以太坊签名算法的原理和应用，我们可以更好地理解以太坊的安全性机制，为区块链技术的发展和应用提供参考。